Definizione
Il test R/S viene comunemente usato per verificare se una serie di dati presenta una
dipendenza a lungo termine. Una delle sue virtù principali è che, a differenza di molti
test statistici usuali non presuppone alcunchè riguardo all'organizzazione dei dati- un
punto critico quando si studia un tema complesso come i prezzi delle azioni, per cui è
ampliamente comprovato che i presupposti tradizionali sono assolutamente sbagliati.
La formula R/S misura semplicemente se, nel corso di intervalli di diversa lunghezza,
la differenza tra valori massimi e minimi dei dati è superiore o inferiore a quella
prevedibile quando ogni dato è indipendente dal precedente.Una sequenza ininterrotta
di guadagni o di perdite spinge necessariamente i valori estremi più in là rispetto a
quelli che si possono realizzare per puro caso. L'equazione per calcolarlo è :
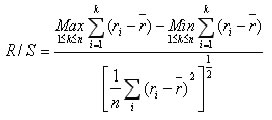
Si inizi a considerare il rendimento r- il guadagno o la perdita derivante dal movimento del prezzo di un'azione in intervalli diversi, di uno, due, tre giorni e così via fino all'intera serie temporali di n giorni, per esempio cento giorni.Si calcola il rendimento medio rn, sull'intero periodo di cento giorni. Poi, per ogni intervallo più breve, un giorno due e così via, si calcola la differenza tra il rendimento rj relativo a quell'intervallo e il rendimento rn, su 100 giorni, continuando a registrare il totale di tutte le differenze via via che gli intervalli crescono fino a tendere a k. Si esegue il calcolo per un solo giorno (K=1),poi per due giorni(K=2) e così via fino a k=100, poi si considera il valore massimo (Max) di tutte queste differenze.In maniera simile si trova il valore Min di tutte le differenze. Sottraendo dal Max il Min si otterrà una stima del campo di variazione dal top all'avvallamento delle deviazioni cumulative per il numeratore. Il denominatore è una misura convenzionale della deviazione standard nelle serie storiche dei dati.Se i dati sono indipendenti , il rapporto tra numeratore e denominatore è ½ ovvero H = 0,5. Per qualsiasi altro valore si rileverà una dipendenza a lungo termine. Se il campo di variazione è maggiore di 0,5 con H > 0,5 allora avremo persistenza dei dati. Per H < 0,5 avremo che i dati saranno antipersistenti e i valori hanno una tendenza a cambiare continuamente direzione.59
[59] E.E. Peters, “ Chaos and Order in the capital markets: A new view of cycles and market volatility” New York 1996
Successivo: Costruire con Matlab il coefficiente di Hurst con la funzione Hurst.m
Sommario: Indice